introduction

To understand the different coding methods, we need to first examine our initial information. Specifically we are going to look at the entropy of our source.

Entropy in our context is the lack of order or predictability in some data. It is the amount of information that is contained in the data and it is also a measure for how much a message can be compressed.

The unit of entropy is bit. To calculate entropy H of a variable X with values x_i with i=1,…,n:

$H( X ) = - \sum_{i=1}^n p_i log_2(p_i)$

With p_i equal to the probability that X holds the value x.

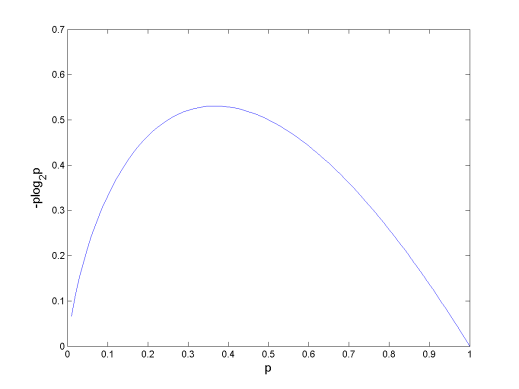
graph of -plog<sub>2</sub>(p) over p shows which values of p contribute the most to entropy — 'graph of -plog₂(p) over p shows which values of p contribute the most to entropy'

The minimum value for entropy is 0. Take note that an event that certainly will or will not occur does not contribute to entropy (because either p_i is 0 or log(1) is 0). And as seen in the graph, events with a probability of approximately 0.4 contribute the most to the entropy.
A variable that is truly random (each possible values is equally likely to occur), has maximum entropy:

$H( X ) = - \sum_{i=1}^n {1\over n} log_2( {1 \over n} ) = log_2 ( n )$

Note: if your calculator doesn’t allow you to do log₂ or if you’re getting tested on this and aren’t allowed to use a calculator that can, remember to convert the bases of log using this formula: $log_b(x) = {log_a(x) \over log_a(b)}$

examples

example 1

Calculate the entropy of a “fair” dice.
$H( X ) = - \sum_{i=1}^n {1\over n} log_2({1 \over n}) = log_2(n)$

show answer

method 1

$H( X ) = log_2(6) = { log_{10}(6) \over log_{10}(2) } = 2.58496$

method 2

$H( X ) = - \sum_{i=1}^n {1 \over 6} log_2({1 \over 6}) = - \sum_{i=1}^n {1 \over 6} {log_{10}({1 \over 6}) \over log_{10}(2)}$
$H( X ) = - (({1 \over 6} * -2.58496)+({1 \over 6} * -2.58496) + ...) = - (({1 \over 6} * -2.58496) * 6) = - (- 2.58496) = 2.58496$

With method 2 you can clearly see why we can simplify the formula to $H( X ) = log_2(n)$ for events that all have the same probability.

example 2

Calculate the entropy of a dice with the probability of 0.5 for the value 3 and an equally distributed probability for the other values. $H( X ) = - \sum_{i=1}^n p_i log_2(p_i)$

show answer

$p_3 = 0.5$ and $p_{1-6} = {0.5 \over 5}$
$H( X ) = - (0.5 * log_2(0.5) + ({1 \over 10} * log_2({1 \over 10}))* 5)$ $H( X ) = - (-0.5 + (-0.332192*5)) = - (-0.5 + (-1.660964)) = 2.1609$

The chance of the dice being anything but 3 is 1-p₃ so 0.5, we divide the chance of that happening equally between the remaining numbers (there are 5 remaining numbers).